三角形勾股定理怎么算目录
三角形勾股定理怎么算

仅适用于。
勾股定理表达式:a+b=c。
勾股定理的公式是:在一个直角三角形中,斜边边长的平方等于两条直角边边长平方之和.如果直角三角形两直角边分别为a、b,斜边为c,那么a的平方+b的平方=c的平方。
意义
1、勾股定理的证明是论证几何的发端。
2、勾股定理是历史上第一个把数与形联系起来的定理,即它是第一个把几何与代数联系起来的定理。
3、勾股定理导致了无理数的发现,引起第一次数学危机,大大加深了人们的理解。
4、勾股定理是历史上第—个给出了完全解答的,它引出了。
5、勾股定理是欧氏几何的基础定理,并有巨大的实用价值。
这条定理不仅在几何学中是一颗光彩夺目的明珠,被誉为“几何学的基石”,而且在和其他科学领域也有着广泛的应用。
勾股定理是什么。怎么计算?
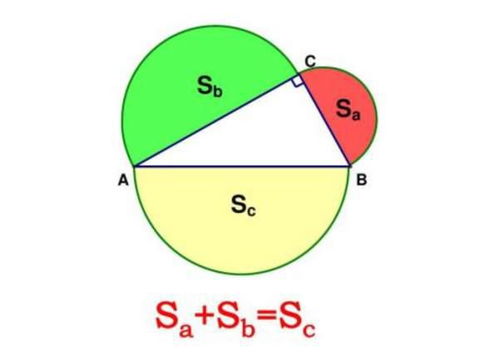
勾股定理是阐述直角三角形三条边的大小关系的一个定理。
勾股定理的语言叙述为:直角三角形中斜边的平方等于两条直角边的平方之和。
勾股定理的表达式为:c^2=a^2+b^2 (其中c表示斜边,a, b分别表示两条直角边)。
勾股定理的用途:主要是用来解“在直角三角形中,已知两边,求第三边”这一类的问题。
三角形勾股定理怎么算 要详细过程
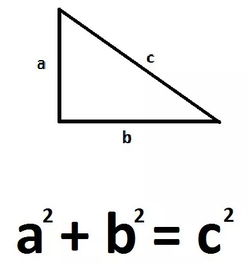
三角形的可以通过公式a+b=c来计算。
勾股定理的定义为:的两条直角边的平方和等于的平方。
即勾股定理的为A+B=C,或者也可以写为C=√(A+B)。
中国古代称直角三角形为勾股形,并且直角边中较小者为勾,另一长直角边为股,斜边为弦,所以称这个定理为勾股定理。
使用勾股定理解决三角形计算的问题方法如下:例如直角三角形 的三条边是3(直角边)、4(直角边)、5(斜边)则3+4=5,可得5=√(3+4)=√5=5。
三角形勾股定理的推论,组是满足勾股定理的正整数组,其中的称为勾股数。
扩展资料勾股定理的证明方法:
在直角梯形ABDE中,∠AEC=∠CDB=90°,△AEC≌△CDB,
,,
∵
参考资料:百度百科—勾股定理
标签:




