内接三角形性质目录
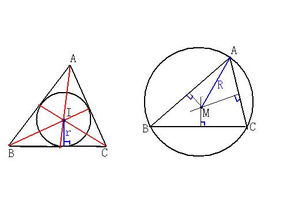
内接三角形性质
。
404 Not Found
。
。
。
。
。
。
。
。
圆内接三角形的性质
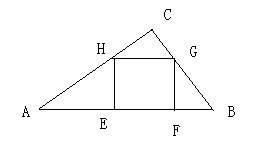
1.在同圆内,等边三角形将圆分成相等的三段弧。
三角形的三个顶点为圆的三等分点。
2.三角形的一个角等于它所对的边与圆心相连所形成的夹角的一半
圆内接三角形有甚麼性质?
圆内接三角形的一个性质及应用
五方向 王永梅
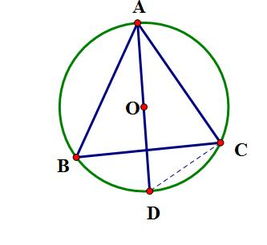
性质:三角形任意两边的乘积等于第三边上的高与其外接圆直径的乘积。
已知圆O是△ABC的外接圆,AD是边BC上的高,AE是圆O的直径。
求证:AB·AC=AD·AE。
证明:如图1所示,连结BE,则有
图1
又AD上是边BC上的高,
所以
故
即
因此,AB·AC=AD·AE。
该性质应用非常广泛,巧妙地应用此性质解题,能简化解题过程。
现举例说明如下:
1. 证明等积式
例1. 如图2所示,已知AB为圆O的一条弦,C、D在圆O上且在AB的同侧,求证:AD·BD·CE=AC·BC·DF。
图2
证明:设圆O的直径为d,则
AD·BD=DF·d
AC·BC=CE·d
两式相乘得
AD·BD·CE·d=AC·BC·DF·d
即
2. 证明比例式
例2. 已知圆O的内接四边形ABCD的对角线BD平分AC于E。
求证;。
证明:如图3所示,分别过点A、C作。
图3
设圆O的直径为d,则
3. 证明定值
例3. 两圆相交于两点A、B,经过交点B的任意一直线和两圆分别相交于点C、D。
求证:AC与AD的比为定值。
证明:如图4所示,连结AB,过A作
图4
设圆O1、圆O2的直径分别为,则,两式相除,得(为定值)。
4. 求函数式
例4. 如图5所示,已知圆O的内接△ABC中,AB+AC=12,且AD=3。
设圆O的半径为y,AB的长为x。
求y与x之间的函数关系式,并指出自变量x的取值范围。
图5
解:连结AO,并延长交圆O于E,则
因为△ABD、△ACD均为直角三角形,且
AD=3,所以
即自变量x的取值范围是。
练习:
已知AC、BD是圆O的内接四边形的两条e68a84e799bee5baa631333330323866对角线,且。
求证:是定值。
内接三角形的性质

内接圆的圆心是由三角形三条边的中垂线(两条就够了,画第3条是检验什么准确)焦点确定的,圆心到三角形3边距离相等(圆的半径)
标签:




