对数函数性质目录qkD高三网

数学对数函数性质qkD高三网

对数函数性质问题qkD高三网

对数函数有那些性质呢？qkD高三网

1. 对数函数的定义域为正实数集合，值域为实数集合。nn2. 对数函数的图像是一条单调递增的曲线，它与x轴交于x=1处。nn3. 对数函数的反函数为指数函数，即y=a^x。nn4. 对数函数的底数越大，其图像越陡峭；底数越小，其图像越平缓。nn5. 对数函数的性质可以用换底公式、对数乘法公式、对数除法公式等方便地计算。nn6. 对数函数在数学、物理、化学等领域中有广泛的应用，如测量震级、pH值、音量等。"

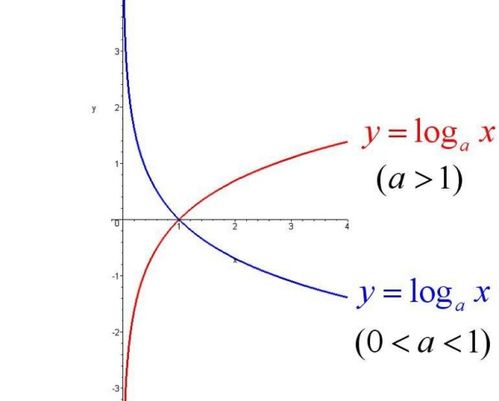
数学对数函数性质

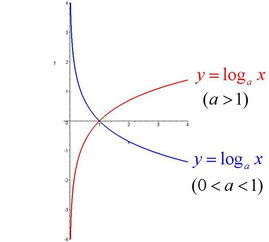
基本性质： qkD高三网

1、a^(log(a)(b))=b qkD高三网

2、log(a)(a^b)=bqkD高三网

3、log(a)(MN)=log(a)(M)+log(a)(N); qkD高三网

4、log(a)(M÷N)=log(a)(M)-log(a)(N); qkD高三网

5、log(a)(M^n)=nlog(a)(M) qkD高三网

6、log(a^n)M=1/nlog(a)(M)qkD高三网

其他性质：qkD高三网

1.换底公式qkD高三网

log(a)(N)=log(b)(N)÷log(b)(a)qkD高三网

2.log(a)(b)=1/log(b)(a)qkD高三网

3.对数函数的图象都过(1,0)点.qkD高三网

4.对于y=log(a)(n)函数, qkD高三网

①,当0<a<1时,图象上函数显示为(0,+∞)单减.随着a 的增大,图象逐渐以(1,0)点为轴顺时针转动,但不超过X=1.qkD高三网

②当a>1时,图象上显示函数为(0,+∞)单增,随着a的增大,图象逐渐以(1.0)点为轴逆时针转动,但不超过X=1.qkD高三网

5.与其他函数与反函数之间图象关系相同,对数函数和指数函数的图象关于直线y=x对称.qkD高三网

对数函数性质问题

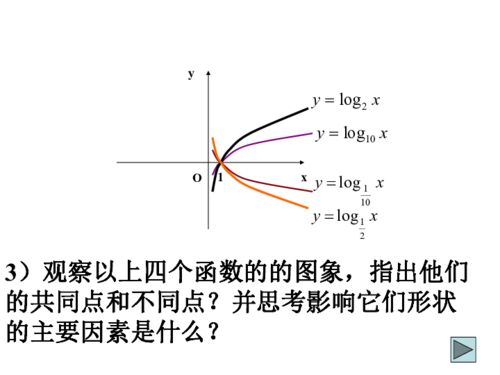
性质1中对数函数的图像仅指 loga(底)xqkD高三网

即 x的取值范围(也就是函数loga(底)x的定义域)为 0到正无穷qkD高三网

对数函数仅要求真数大于0, 而不是x大于0, 这点很重要!qkD高三网

所以对loga(底)x^2来说, x的取值范围为x^2从0到正无穷, 即函数的定义域是qkD高三网

0 < x^2 < 正无穷qkD高三网

满足这个条件的x只要不为0就行了, 所以x的取值范围(也就是函数的定义域)是(-无穷大，0)并（0，正无穷大）qkD高三网

对数函数有那些性质呢？

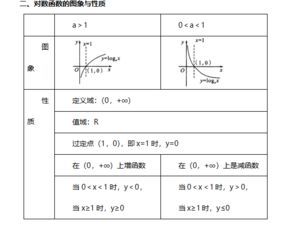
1. 定义域：对数函数y=log ax 的定义域是{x 丨x>0}；qkD高三网

2. 值域 ： 实数集R，显然对数函数无界； qkD高三网

3. 定点 ：对数函数的函数图像恒过定点（1，0）； qkD高三网

4. 单调性 ：a>1时，在定义域上为单调增函数； 0<a<1时，在 定义域上为单调减函数； qkD高三网

5. 奇偶性 ： 非奇非偶函数； qkD高三网

6. 周期性 ：不是 周期函数 ；qkD高三网

7. 对称性：无 ；qkD高三网

8. 最值：无 ；qkD高三网

9. 零点：x=1；qkD高三网

10. 拓展资料：（1）常用对数：lg(b)=log 10b（10为底数）；qkD高三网

（2） 自然对数：ln(b)=log eb（e为底数） e为 无限不循环小数，通常情况下只取e=2.71828。

标签：