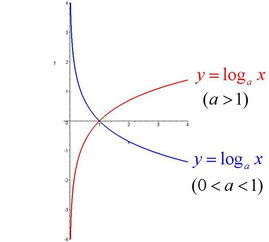
对数函数的导数目录1A5高三网

对数函数的导数1A5高三网

对数函数的导数的证明1A5高三网

对数函数的导数公式为：nn$$frac{d}{dx}ln x = frac{1}{x}$$nn其中，$ln x$ 表示以 $e$ 为底数的对数函数。"

对数函数的导数

这是个复合函数，即y=ln[f(x)]，其中f(x)=2x^2+3x+1也就是说该函数是由一个对数函数和一个二次函数复合而成的函数，其中对数函数为主体函数，二次函数为附加函数，因此在求复合函数的导数的时候不能只求主体函数的导数，还要求整个复合函数的导数1A5高三网

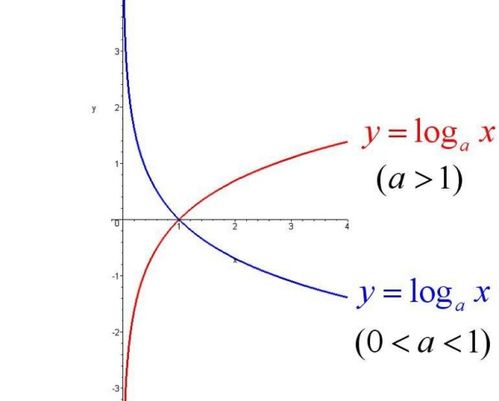
对数函数的导数的证明

对数函数的导数的证明 1A5高三网

利用反函数求导1A5高三网

设y=loga(x) 则x=a^y1A5高三网

根据指数函数的求导公式，两边x对y求导得:1A5高三网

dx/dy=a^y(lna)1A5高三网

所以1A5高三网

dy/dx=1/[a^y(lna)]（将x=a^y代入）1A5高三网

=1/(xlna)

标签：